敏捷估算︱一文深度剖析故事点估算

比如：
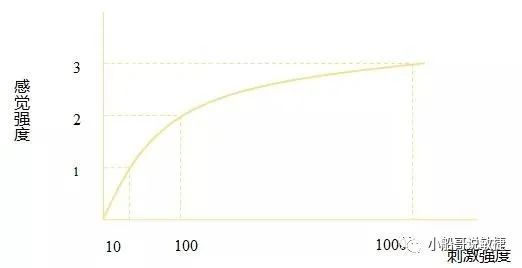
我们大部分人都能分辨出1公斤和2公斤物体，但可能无法分辨出20公斤和21公斤物品。它们同样是相差了1公斤，为什么有的能分辨出来，有的就分辨不出来了呢？这是因为1公斤和2公斤之间的差别是100％，但是20公斤和21公斤之间的差异仅为5％，20公斤和21公斤之间的百分比差异太小了。这就是韦伯定律想要告诉我们的：差异太小，我们是分辨不出来的；只有差异大到一定程度，才能被我们分辨。那人们可以分辨出多大比例的差异呢？
 
2.2. 人们可以分辨出的差异比例
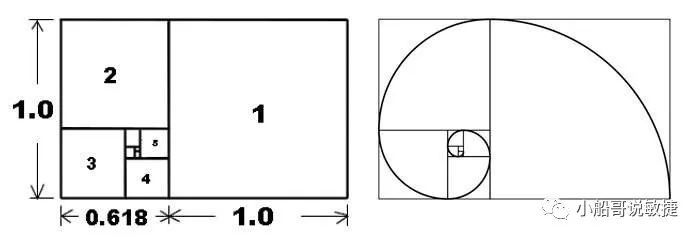
韦伯定律只是告诉了我们可以识别一定百分比差异外的区别，但是这个百分比是多少呢？自然界有个神奇的数字：0.618，即黄金分割比例。
 
黄金分割比例的现象在我们身边有很多，比如：
人们的肚脐是人体总长的黄金分割点
大多数门窗的宽长之比也是0.618
有些植茎上，两张相邻叶柄的夹角是137°28'，这恰好是把圆周分成1:0.618
一些名画、雕塑、摄影作品的主题，大多在画面的0.618处
……
甚至在医学领域，当一个患者报告说自己感受到了病情的好转，那么实际上他的病已经好了65%。也就是说，61.8%这个百分比差异对很多人来说，是可以轻易分辨出来的。
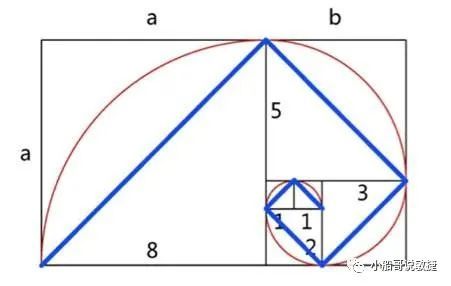
2.3. 斐波那契数列大致符合了黄金分割比例
斐波那契数列之所以能很好的用于故事点的估算，是因为该数列的数字分布大致符合了黄金分割比例。在这个数列中，1、2、3、5、8、13、21……，前两个值（后一个值比前一个值大100％）之后，后面的每个数字都比前一个数字值大60％左右。

根据韦伯定律，
 
如果我们可以区分两个工作量相差60％的故事，则可以区分其他相同百分比差异的故事。因此，斐波那契值之所以能很好地工作，是因为它们每次都以大约相同的比例增加，且该比例基本符合黄金分割比例。
 
3. 为什么敏捷估算要使用修正后的斐波那契数列
标准的斐波那契数列是1、2、3、5、8、13、21、34、55……，但是目前绝大多数团队在估算时使用的斐波那契数列是1、2、3、5、8、13、20、40、100……，数列的前面6个数字是一样的，但是从第7个数字开始，就完全不一样了，这是为什么呢？Mike Cohn曾经在他的文章中提到，早期的估算他都是根据真实的斐波那契数列进行的（1、2、3、5、8、13、21、34、55……）。这个数列越往后数字越大，也就说明估算越不准确，所以对于21、34、55这样的估算值，很多人都觉得很奇怪：既然已经估不准了，为什么非要使用21，而不将其四舍五入为20或25呢？于是Mike Cohn就接受了这个建议，在之后的团队辅导及授课中他就开始使用20而不是21了，并且一直持续到了现在。后来他又尝试使用了40和100这两个数代替了数列的其他值，之所以这么使用，是因为任务的粒度越粗，估算就越不准确，也就越不需要纠结到底是80、90还是100了。同时，使用40和100也是不违反韦伯定律的，它们分别比之前的数字增加了100％（20 →40）和150％（40 →100）。这比黄金分割比例的61.8％大得多，人们是可以轻松的分辨出这些工作量的区别的。后来在Mike Cohn的影响下，现在大部分公司在敏捷估算中都开始使用修正后的斐波那契数列了：1、2、3、5、8、13、20、40、100、∞。
 
4. 为什么要使用规划扑克
 
相信很多人在估算故事点时，都是使用物理或电子的规划扑克进行的，我们为什么要这么做呢？这个问题需要从一个心理学名词“从众效应”说起。
4.1. 什么是从众效应
在估算故事点时，当有人提出一个估算，即使你不同意，但当别人都表达赞同时，你还是会随声附和，这就是所谓的“从众效应”：人们认为如果其他人都赞同某一件事时，那么自己的保留意见则是愚蠢的或是误导性的，他们不想在其他人面前出丑。这个弱点不是个体独有的，而是全人类共有的。